Overview of geometric optimization methods.Abstract
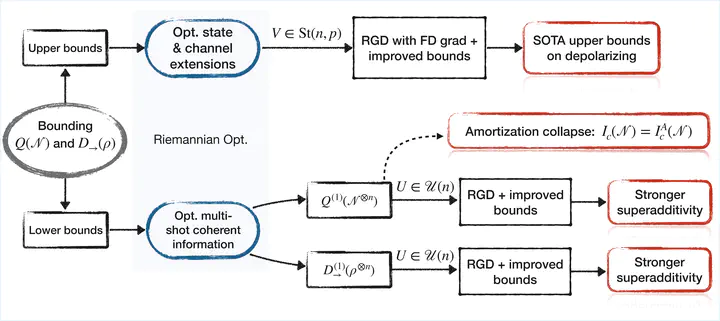
Determining the ultimate limits of quantum communication, such as the quantum capacity of a channel and the distillable entanglement of a shared state, remains a central challenge in quantum information theory, primarily due to the phenomenon of superadditivity. This work develops Riemannian optimization methods to establish significantly tighter, computable two-sided bounds on these fundamental quantities.
For upper bounds, our method systematically searches for state and channel extensions that minimize known information-theoretic bounds. We achieve this by parameterizing the space of all possible extensions as a Stiefel manifold, enabling a universal search that overcomes the limitations of ad-hoc constructions. Combined with an improved upper bound on the one-way distillable entanglement based on a refined continuity bound on quantum conditional entropy, our approach yields new state-of-the-art upper bounds on the quantum capacity of the qubit depolarizing channel for large values of the depolarizing parameter, strictly improving the previously best-known bounds.
For lower bounds, we introduce Riemannian optimization methods to compute multi-shot coherent information. We establish lower bounds on the one-way distillable entanglement by parameterizing quantum instruments on the unitary manifold, and on the quantum capacity by parameterizing code states with a product of unitary manifolds. Numerical results for noisy entangled states and different channels demonstrate that our methods successfully unlock superadditive gains, improving previous results. Together, these findings establish Riemannian optimization as a principled and powerful tool for navigating the complex landscape of quantum communication limits. Furthermore, we prove that amortization does not enhance the channel coherent information, thereby closing a potential avenue for improving capacity lower bounds in general. This result can be of independent interest.
Chengkai Zhu
PhD Student (2023)
I obtained my BS in Applied Mathematics from China Agricultural University under the supervision of Prof. Zhencai Shen. I obtained my MS degree in Cyberspace Security from University of Chinese Academy of Sciences under the supervision of Prof. Zhenyu Huang. My research interests include quantum information theory and quantum computation.
Xin Wang
Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.