Abstract
Identifying symmetries in quantum dynamics, such as identity or time-reversal invariance, is a crucial challenge with profound implications for quantum technologies. We introduce a unified framework combining group representation theory and subgroup hypothesis testing to predict these symmetries with optimal efficiency. By exploiting the inherent symmetry of compact groups and their irreducible representations, we derive an exact characterization of the optimal type-II error (failure probability to detect a symmetry), offering an operational interpretation for the quantum max-relative entropy. In particular, we prove that parallel strategies achieve the same performance as adaptive or indefinite-causal-order protocols, resolving debates about the necessity of complex control sequences. Applications to the singleton group, maximal commutative group, and orthogonal group yield explicit results: for predicting the identity property, Z-symmetry, and T-symmetry of unknown qubit unitaries, with zero type-I error and type-II error bounded by , we establish the explicit optimal sample complexity which scales as for identity testing and for T/Z-symmetry testing. These findings offer theoretical insights and practical guidelines for efficient unitary property testing and symmetry-driven protocols in quantum information processing.
Publication
arXiv:2502.01464

Research Associate
I obtained my BS in Mathematics and Applied Mathematics from University of Science and Technology of China. I obtained my PhD degree in Applied Mathematics from University of Chinese Academy of Sciences under the supervision of Prof. Xiao-Shan Gao. My research interests include quantum computing, symbolic computation and cryptanalysis.

PhD Student (2023)
I obtained my BS and MS degrees in computer science from the University of Melbourne. My research interests include distributed quantum computing, quantum entanglement and quantum machine learning.

Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.
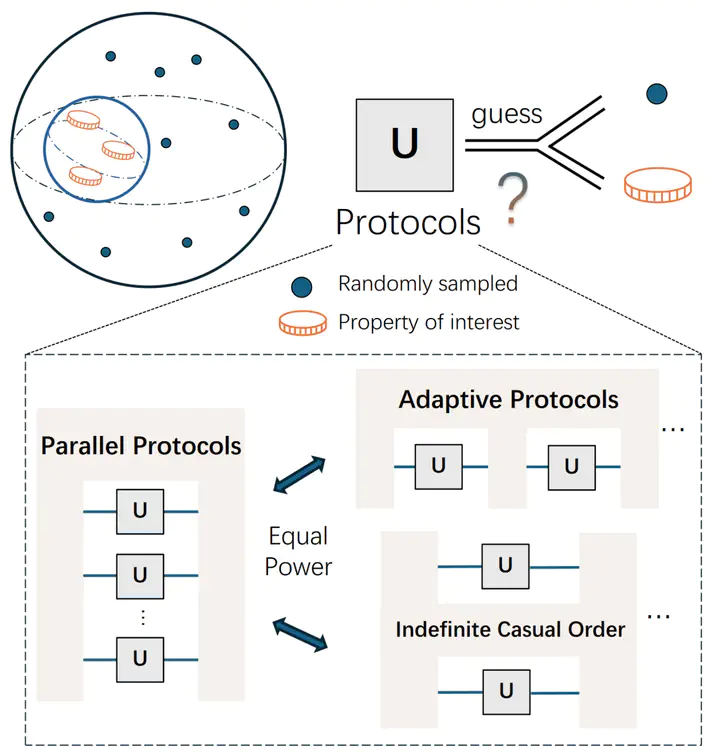 Hypothesis testing for quantum dynamics
Hypothesis testing for quantum dynamics