Quantum State Discrimination¶

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview¶

Quantum state discrimination (QSD) [1-2] is a fundamental question in quantum communication, quantum computation, and quantum cryptography. In this tutorial, we will explain how to discriminate two orthogonal bipartite pure states |ψ⟩|ψ⟩ and |ϕ⟩|ϕ⟩, which satisfies ⟨ψ|ϕ⟩=0⟨ψ|ϕ⟩=0, under the constraint of Local Operations and Classical Communication (LOCC). We refer all the theoretical details to the original paper [3].

QSD Protocol¶

Firstly, we want to make the problem definition clear. Consider two spatially separated parties AA (Alice) and BB (Bob) sharing a given two-qubit system. The system state is |φ⟩|φ⟩ previously distributed by another party CC (Charlie). Alice and Bob were only notified that |φ⟩|φ⟩ is either |ψ⟩|ψ⟩ or |ϕ⟩|ϕ⟩ (both are pure states), satisfying ⟨ψ|ϕ⟩=0⟨ψ|ϕ⟩=0. Then, Charlie provides many copies of |ψ⟩|ψ⟩ and |ϕ⟩|ϕ⟩ to them, and he asks Alice and Bob to cooperate with each other to figure out which state they are actually sharing.

Solving this problem under our LOCCNet framework is trivial. As always, let's start with the simplest one-round LOCC protocol with a QNN architecture shown in Figure 1. Then, the difficulty lies in the design of an appropriate loss function LL. Since we choose to let both parties measure their subsystem, there will be four possible measurement results mAmB∈{00,01,10,11}mAmB∈{00,01,10,11}. To distinguish |ψ⟩|ψ⟩ and |ϕ⟩|ϕ⟩, we will label the former state with measurement results mAmB∈{00,10}mAmB∈{00,10} and the latter with mAmB∈{01,11}mAmB∈{01,11}. This step can be understood as adding labels to the data in supervised learning. With these labels, we can define the loss function as the probability of guessing wrong label,

L=p|ψ⟩_01+p|ψ⟩_11+p|ϕ⟩_10+p|ϕ⟩_00,(1)(1)L=p|ψ⟩_01+p|ψ⟩_11+p|ϕ⟩_10+p|ϕ⟩_00,

where p|ψ⟩_01p|ψ⟩_01 stands for the probability of measuring 01 when the input state is |ψ⟩|ψ⟩. Then we can begin the training stage to minimize the loss function.

qsd

Figure 1: Schematic diagram of state discrimination with LOCCNet.

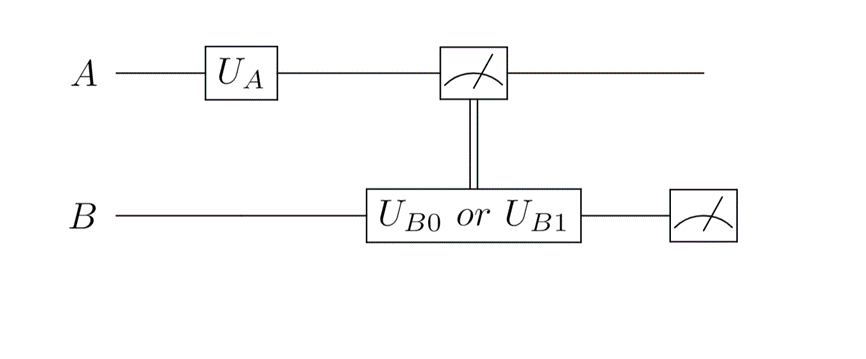
We summarize the workflow below:

  1. Alice and Bob share a two-qubit system, which state is either |ψ⟩|ψ⟩ or |ϕ⟩|ϕ⟩.
  2. Alice operates a general rotation gate UAUA on her qubit.
  3. Alice measures her qubit on the computational basis, and the result mA∈{0,1}mA∈{0,1}. Then, she communicates with Bob about the measurement result through a classical channel.
  4. Bob operates different gates on his qubit depending on Alice's measurement result. If, mA=0mA=0 Bob acts UB0UB0 on his qubit; If mA=1mA=1, then Bob acts UB1UB1. Then, Bob measures his qubit and obtain mB∈{0,1}mB∈{0,1}. Note: Both UB0UB0 and UB1UB1 are universal single-qubit gate u3().
  5. Calculate the loss function L=p|ψ⟩_01+p|ψ⟩_11+p|ϕ⟩_10+p|ϕ⟩_00L=p|ψ⟩_01+p|ψ⟩_11+p|ϕ⟩_10+p|ϕ⟩_00, and use gradient-based optimization methods to minimize it.
  6. Repeat 1-5 until the loss function converges.
  7. Input the pre-shared state |φ⟩|φ⟩ to make a decision and compare with Charlie's answer.

Simulation with Paddle Quantum¶

First, import relevant packages.

In [2]:
import numpy as np
from scipy.stats import unitary_group
import paddle
import paddle_quantum
from paddle_quantum.locc import LoccNet
# Change to density matrix mode
paddle_quantum.set_backend('density_matrix')

Randomly generate two orthogonal pure states |ψ⟩|ψ⟩ and |ϕ⟩|ϕ⟩ by Charlie.

In [3]:
def states_orthogonal_random(n, num=2):
    # Randomly generate two orthogonal states
    assert num <= 2 ** n, "return too many orthognal states"
    U = unitary_group.rvs(2 ** n)
    return_list = [np.array(U[i], dtype=np.complex64) for i in range(num)]

    return return_list

Below is the main part of our LOCC protocol:

In [4]:
class Net(LoccNet):
    def __init__(self):
        super(Net, self).__init__()
        # Add the first party Alice 
        # The first parameter 1 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(1, party_name='Alice')
        # Add the first party Bob 
        # The first parameter 1 stands for how many qubits B holds
        # The second parameter records the name of this party
        self.add_new_party(1, party_name='Bob')

        # Rewrite the input states into density matrices
        _states = states_orthogonal_random(2)
        _states = [paddle_quantum.State(np.outer(init_state, init_state.conjugate())) for init_state in _states]
        # Initialize the system by distributing states
        self.set_init_state(_states[0], [('Alice', 0), ('Bob', 0)])
        self.psi = self.init_status
        self.phi = self.reset_state(self.init_status, _states[1], [('Alice', 0), ('Bob', 0)])

        # Alice's local operations
        self.cirA = self.create_ansatz('Alice')
        # Add single-qubit universal gate
        self.cirA.u3(0)
        # Bob has to prepare two circuits according Alice's measurement result
        self.cirB = [self.create_ansatz('Bob'), self.create_ansatz('Bob')]
        # Add single-qubit universal gate
        self.cirB[0].u3(0)
        self.cirB[1].u3(0)

    def run_circuit(self, party, cir, state, res):
        # Run circuit
        after_state = cir(state)
        # Measure the circuit and record the measurement results 
        after_state = self.measure(status=after_state, which_qubits=(party, 0), results_desired=res)

        return after_state

    def forward(self):
        # Training steps
        # Quantum state after Alice's operation
        psi = self.run_circuit('Alice', self.cirA, self.psi, ['0', '1'])
        phi = self.run_circuit('Alice', self.cirA, self.phi, ['0', '1'])

        # Calculate the loss function
        loss = 0
        for each_psi in psi:
            if each_psi.measured_result == '0':
                psi_01 = self.run_circuit('Bob', self.cirB[0], each_psi, '1')
                loss += psi_01.prob
            elif each_psi.measured_result == '1':
                psi_11 = self.run_circuit('Bob', self.cirB[1], each_psi, '1')
                loss += psi_11.prob
        for each_phi in phi:
            if each_phi.measured_result == '0':
                phi_00 = self.run_circuit('Bob', self.cirB[0], each_phi, '0')
                loss += phi_00.prob
            elif each_phi.measured_result == '1':
                phi_10 = self.run_circuit('Bob', self.cirB[1], each_phi, '0')
                loss += phi_10.prob

        return loss

    def evaluate(self):
        # Test step
        choice = np.random.choice(['phi', 'psi'])
        if choice == 'phi':
            self.status = self.phi
        else:
            self.status = self.psi
        print('Charlie chooses the state', choice)

        # Alice's operations
        status = self.run_circuit('Alice', self.cirA, self.status, ['0', '1'])
        # Bob's operations 
        result_0 = list()
        result_1 = list()
        for each_status in status:
            if each_status.measured_result == '0':
                status = self.run_circuit('Bob', self.cirB[0], each_status, ['0', '1'])
                result_0.append(status[0].prob.numpy()[0])
                result_0.append(status[1].prob.numpy()[0])
            elif each_status.measured_result == '1':
                status = self.run_circuit('Bob', self.cirB[1], each_status, ['0', '1'])
                result_1.append(status[0].prob.numpy()[0])
                result_1.append(status[1].prob.numpy()[0])

        print("The probability that Alice and Bob recognize it as psi:", result_0[0] + result_1[0])
        print("The probability that Alice and Bob recognize it as phi:", result_0[1] + result_1[1])

Train the QNN parameters, and Charlie randomly select one of the two orthogonal states |ψ⟩|ψ⟩ and |ϕ⟩|ϕ⟩ and see whether Alice and Bob can distinguish it correctly.

In [6]:
ITR = 100  # Set the number of training iterations
LR = 0.1   # Set learning rate
SEED = 999 # Fix randome seed for parameters in PQC
np.random.seed(SEED)
paddle.seed(SEED)

net = Net()
params = net.cirA.parameters() + net.cirB[0].parameters() + net.cirB[1].parameters()
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=params)
# Train the LOCC net for ITR iterations by gradient descent
for itr in range(ITR):
    loss = net()
    loss.backward()
    opt.minimize(loss)
    opt.clear_grad()
    if itr % 10 == 0:
        print("itr " + str(itr) + ":", loss.numpy()[0])
print("Minimum loss:", loss.numpy()[0])

print("======================== test stage ===============================")
np.random.seed(10)
net.evaluate()
np.random.seed(6)
net.evaluate()

itr 0: 1.1238832
itr 10: 0.32665575
itr 20: 0.085007355
itr 30: 0.085270524
itr 40: 0.026622297
itr 50: 0.015240545
itr 60: 0.007836903
itr 70: 0.004827206
itr 80: 0.0035075857
itr 90: 0.002215183
Minimum loss: 0.0016813411
======================== test stage ===============================
Charlie chooses the state psi
The probability that Alice and Bob recognize it as psi: 0.9990063
The probability that Alice and Bob recognize it as phi: 0.0009937042
Charlie chooses the state phi
The probability that Alice and Bob recognize it as psi: 0.0006236615
The probability that Alice and Bob recognize it as phi: 0.9993763

Conclusion¶

It can be seen from the simulation results that the trained quantum circuit can distinguish two orthogonal quantum states almost perfectly with an accuracy >99.9%>99.9%. There is an interesting question that can we generalize this discrimination scheme by adding more states to the category.

References¶

[1] Barnett, Stephen M., and Sarah Croke. "Quantum state discrimination." Advances in Optics and Photonics 1.2 (2009): 238-278.

[2] Chefles, Anthony. "Quantum state discrimination." Contemporary Physics 41.6 (2000): 401-424.

[3] Walgate, Jonathan, et al. "Local distinguishability of multipartite orthogonal quantum states." Physical Review Letters 85.23 (2000): 4972.